PAL vs NTSC Timer Increment
In NTSC (60Hz), the internal race timer is incremented by 0.016666666 each frame.
In PAL (50Hz), you would expect the race timer to be incremented by 0.02 each frame, but it's actually incremented by 0.020041666 (this value is hardcoded into the game).

By dividing these two values, you can see the game has a conversion rate of 1.2025000. That is, you move the same distance each frame whether you are playing NTSC or PAL, but the clock is intended to increment 1.2025 times faster in PAL.

Mechanism for incrementing timer
The game stores the race timer as a single-precision (4 bytes) floating point number. Each frame, it is read from memory, then converted to a double-precision floating point number, then the increment value discussed above is added (depending on whether you're in PAL or NTSC), then the number is converted back to single precision and stored in memory.

Display timer
The timer displayed during the race only shows your time to the hundredths of a second. To generate this time, the internal race timer is multiplied by 100, and then truncated (rounded down) to an integer. This integer is then displayed on the timer.

Floating-point rounding errors cause inconsistent timer rate and conversion rate
A single-precision floating point number is (1+(fraction))*2^(exponent), where (fraction) represents a number between 0 and 1 and takes up 23 bits and (exponent) takes up 8 bits. As a result, for numbers between 2ⁿ and 2⁽ⁿ⁺¹⁾ the spacing between consecutive single-precision floating point number is 2^(n-23).
Let's Use n=6 as an example. Between 64 and 128 seconds, the spacing between single-precision floating point numbers is 2^-17. This means that when we try to increment by 0.01666667 seconds to get to the next frame, that should be increasing the timer by 0.01666667/(2^-17) = 2184.53377 times the smallest possible increment. Instead, the single-precision float can only be incremented by either 2184*(2^-17) or 2185*(2^-17). Due to the rounding rules for converting double-precision floats to single-precision floats, it ends up being 2185 times the increment.

So we wanted the timer to advance by 0.0166666667 seconds (or 2184.53377 * 2^-17), but instead it increments by 0.01667023.

Over 2400 frames, that means we the game tried to advance the timer by 40 seconds, but it ended up advancing by 40.008545 seconds, or almost 0.01 more than expected. Assuming the game does a good job calculating precise lap start and finish times from how far you go over the line during the lap change frame, these conversion rates between NTSC and PAL should be accurate.

In general, the rounding errors increase over time We showed that between 64 seconds and 128 seconds, the error was approximately 2^-17 seconds per frame. When the timer is at larger values, this error per frame will also increase (due to the spacing between consecutive floating point numbers increasing). Depending on the rounding, the timer may increase faster or slower than expected, but the magnitude of the error will generally increase as you move to bigger exponents. For example, between 2¹² and 2¹³ seconds (~ 1-2 hours into the race), the error per frame will be on the order of 2^-11 (~1/2000) seconds. Over a 2400 frame lap, that'd be an error of 1.2 seconds. Note: These are worst-case values for the rounding error. I think on average it'd be 4 times smaller. The worst case rounding would be rounding 0.99 to 0 for example. But if rounds to the nearest integer then you'd expect an average case rounding error to be 0.75 to 1, for a correction of 0.25.

Calculation of lap time
You arrive at the finish line sometime between frame n and frame n+1. The game does some computation to determine the time when you crossed the finish line. More investigation is needed into this computation.

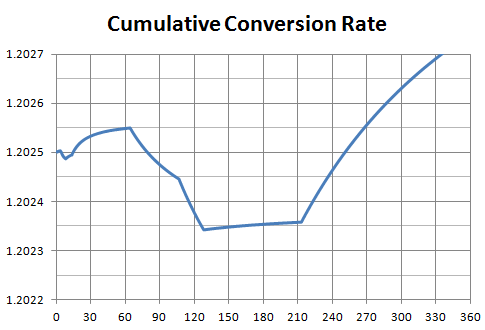
Conversion Rate
The plot below shows what the conversion rate should be for 3lap races of various lengths so that races which used the same number of frames will be rewarded with the same times.


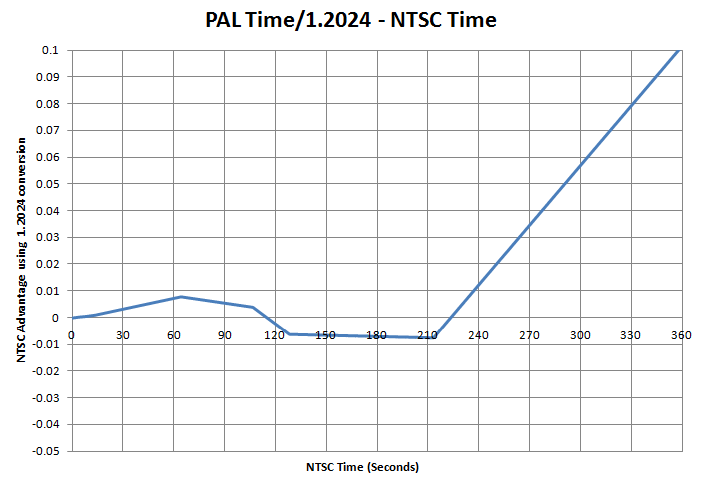
Bias from using 1.2024 as conversion rate
The plot below shows which system is advantaged in 3lap races by the current 1.2024 conversion rate, and by how much.


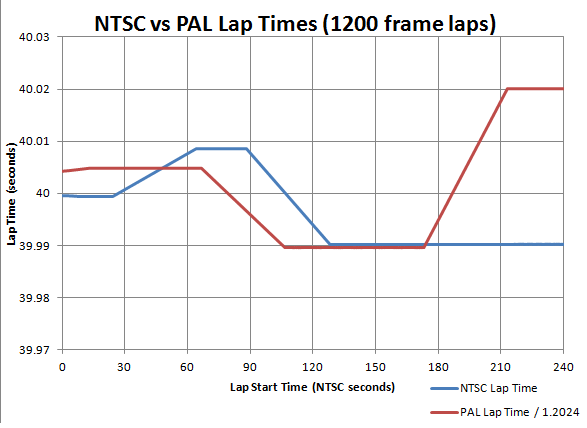
Lap Times impacted by Lap Start Time The plot below shows what time you'll get if you complete a lap in 1200 frames, as a function of when you started the lap.

The plot below shows the same sort of plot as before, but on a much longer time scale, showing the errors growing dramatically over time. After 4-5 days, the timer stops incrementing completely, since the increment values (0.016 or 0.02) are smaller than the distance between consecutive single-precision floating point numbers bigger than 2^19 (524288 seconds)